There are several interesting papers on the arXiv today. One of them, arXiv:2507.15949, involves my former PhD supervisor. It's on the subject of Quantum Entanglement at collider experiments, and relates back to a paper of his from 1992 that I didn't know about (there's a great line in the new paper where the authors complain that their earlier paper was ignored). (Quantum) Entanglement is the phenomenon where two or more particles are in a special state so that their properties are related, but we don't know what those properties are until we measure them. In Quantum Mechanics we would say that the actual state is not decided until we measure them, and this leads to 'spooky action at a distance' because by measuring one particle we appear to set the corresponding property of the other. An alternative explanation would be that there is some hidden quantity or 'hidden variable' where both particles secretly know all along what state they are in. However, surprisingly it's possible to discriminate between these two cases, and set up quantitative tests known as 'Bell inequalities': you can make a measurement and, if the result of that measurement is less than a certain value, then a hidden variable theory cannot explain it. Experiments to test this using photons at low energies were performed in the early 80s by Alain Aspect and others that violated Bell inequalities and thus confirming the Quantum Mechanical interpretation.
In recent years, experimentalists have become interested in performing similar tests using different particles at higher energies; it is legitimate to ask "is this true for fermions?" or "does this break down at high energy?" Apparently similar questions were asked in the early 90s at LEP where electrons and positrons were collided (instead of protons at the LHC) and the 1992 paper pointed out that they were not really testing Bell Inequalities. The new paper revisits the older argument, and applies it to the new case of e.g. proton collisions producing a top-antitop pair. They argue that the quantity of interest for the Bell Inequality is the spin density matrix:
But what can actually be measured is the differential cross-section (the rate of production of particles in a certain angular volume):
The symbols B and C appear in both expressions: when performing experimental tests of Bell inequalities they are identified with each other. Since the differential cross-section can be measured, the measurement for the Bell Inequality can then be made and tested. However, the authors of the new paper claim that, in order to identify the two sets of symbols, it is necessary to use Quantum Field Theory: the second equation is a prediction based on QFT from the first. In other words, the logic is circular, and Quantum Mechanics has been assumed -- so it's not surprising that the Bell inequality is violated!I haven't worked on this topic myself, so it will be interesting to see if there is some pushback from the authors of papers such as arXiv:2003.02280 (who proposed such top-antitop studies).
Fermi decay constant -- at three loops!
I also want to point out arXiv:2507.15946 by Stephen Martin, who has performed a three-loop computation of the decay rate of the muon in the Standard Model at three loops. This quantity is incredibly important; it is measured very precisely, and so we use it to extract the underlying parameters of the Standard Model -- or, any theory beyond it. But since it's a complicated process, this is a tricky computation, even at low loop order. The results in this paper will be useful for all sorts of calculations, such as extracting the Higgs boson's self-coupling -- and working out whether the universe is metastable!

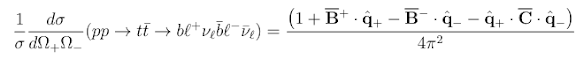
No comments:
Post a Comment